Atcoder Panasonic Programming Contest 2020 题解

A - Kth Term

模拟水题，复制粘贴即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<bits/stdc++.h>
using namespace std;
#define maxn 1010
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#pragma GCC optimize(2)
#define ll long long
#define makefa(n) for(int i=1;i<=(n);i++)f[i]=i;
#define hh puts("");
int main(){
    int a[32]={1, 1, 1, 2, 1, 2, 1, 5, 2, 2, 1, 5, 1, 2, 1, 14, 1, 5, 1, 5, 2, 2, 1, 15, 2, 2, 5, 4, 1, 4, 1, 51};
    int k;
    cin>>k;
    cout<<a[k-1];
    return 0;
}

B - Bishop

看图差不多就能看出规律，奇数行的偶数位走不到，偶数行的奇数位走不到，但要注意特判1，h或w为1时只能是1个（蒟蒻就这wa了五发QAQ）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<bits/stdc++.h>
using namespace std;
#define maxn 1010
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#pragma GCC optimize(2)
#define ll long long
#define makefa(n) for(int i=1;i<=(n);i++)f[i]=i;
#define hh puts("");
int main(){
    ll h,w;
    cin>>h>>w;
    if(w==1||h==1){cout<<"1";return 0;}
    ll x=w/2,y=h/2;
    if(w%2!=0)x++;
    if(h%2!=0)y++;
    ll ans=x*y;
    ans+=(w-x)*(h-y);
    cout<<ans;
    return 0;
}

C - Sqrt Inequality

模拟水题，但是会卡double精度，一开始只把double换成了long double,没有两边平方，两边平方后sqrt/sqrtl求均可（感谢某位大佬指点）

1
2
3
4
5
6
7
8
9
10
11
12
#include<bits/stdc++.h>
using namespace std;
#define ld long double
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);
	ld a,b,c;
	cin>>a>>b>>c;
	if(a+b+2*sqrtl(a*b)<c)cout<<"Yes";
	else cout<<"No";
}

D - String Equivalence

（早知道D这么水我就先做D了）
很明显的一道dfs题，求一个加了限制条件的全排列，对于第k位来说，当前位置最多能放的字母种类一定和之前的位置有关，如果前k-1位放了dif种字母，那么第k位就可以放dif+1种字母，dfs过程中记录dif就好.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<bits/stdc++.h>
using namespace std;
#define maxn 1010
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#pragma GCC optimize(2)
#define ll long long
#define makefa(n) for(int i=1;i<=(n);i++)f[i]=i;
#define hh puts("");
#define eps 1e-10
#define db double
int n;
int dif=0;
char s[maxn];
void dfs(int i){
    if(i==n+1){
        cout<<s+1<<endl;
        return;}
    for (int j = 0; j <=dif ; ++j) {
        s[i]='a'+j;
        int tmp=dif;
        if(j==dif)dif++;
        dfs(i+1);
        dif=tmp;
    }
}
int main(){
    cin>>n;
    dfs(1);
    return 0;
}

E - Three Substrings

dp题
答案可以通过计算a,b,c的相对位置得出，不妨固定a的首字母位置是0，那么b，c的首字母的位置可能是-4000~4000，遍历可能的位置并判断当前位置是否合法，遍历过程中更新答案即可。
怎么找合法位置，比如下图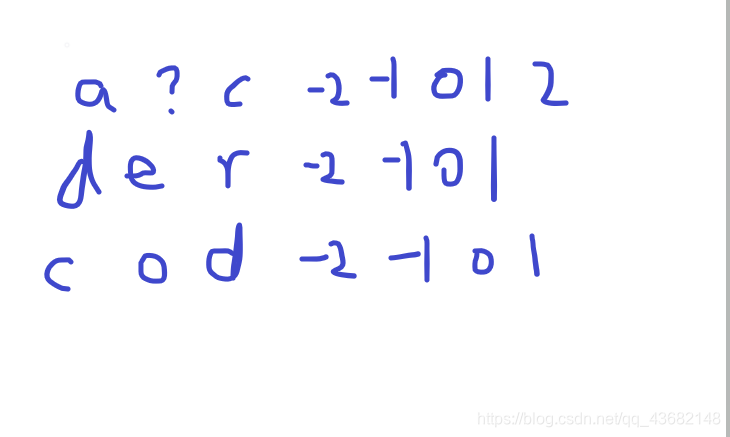
忽略字体QAQ
对于a和b固定a的首字母位置为0，然后两个for判断匹配情况，如果a的第i个字符与b的第j个字符不匹配（不相同或者均不为’?’），那么b的首字母位置就是i-j+0，标记该位置记为不合法情况，依次处理ab，bc，ac（三个数组记录，图中分别是ab，bc，ac，即固定前者的情况下后者的相对位置）。

计算答案时，b相对位置为i，c相对位置为j，则c相对于b的位置为j-i（画图易得）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
#define maxn 2010
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#pragma GCC optimize(2)
#define ll long long
#define makefa(n) for(int i=1;i<=(n);i++)f[i]=i;
#define hh puts("");
#define eps 1e-10
#define db double
#define AC 2333
#define REP(i,n) for((i)=0;(i)<(n);(i)++)
bool ab[maxn+20000],ac[maxn+20000],bc[maxn+20000];
bool match(char c,char d){return c==d||c=='?'||d=='?';}
int main(){
   IOS
   string a,b,c;
   cin>>a>>b>>c;
   int i,j;
   int la=a.size(),lb=b.size(),lc=c.size();
   REP(i,la)REP(j,lb)if(!match(a[i],b[j]))ab[i-j+10000]=true;
    REP(i,la)REP(j,lc)if(!match(a[i],c[j]))ac[i-j+10000]=true;
    REP(i,lb)REP(j,lc)if(!match(b[i],c[j]))bc[i-j+10000]=true;
    int ans=3*maxn;
    for (i = -2*maxn; i <=2*maxn ; ++i) {
        for (j = -2*maxn;  j<=2*maxn ; j++) {
            if(!ab[i+10000] && !ac[j+10000] && !bc[j-i+10000]){
                int l=min(0,min(i,j));
                int r=max(la,max(lb+i,j+lc));
                ans=min(ans,r-l);
            }
        }
    }
    cout<<ans;
    return 0;
}

F - Fractal Shortest Path