Codeforces 每日一练 735D+573B+374C

735D Taxes

传送门
镜像传送门
数论题（1600）
Mr. Funt有收入为n，他为了减少自己需要缴纳的税额（DD行为），想要把收入分成k份（每份收入>1），每份单独缴税。对于每份收入，需要缴纳的税款为其最大因子（不为自己，如果是质数就是1）。帮助Mr. Funt最小化他缴纳的税款。
首先如果n为质数就可以不分了，1一定是最小的。
对于偶数，结果必定大于等于2，分两个质数就是2，分一个两个偶数就大于2，根据哥德巴赫猜想，任一大于2的偶数都可写成两个素数之和，那么偶数的答案就是2。
对于奇数，必定会分成一奇一偶，而偶数小于等于2（2的情况为1），而且一定可以找到一个质数充当分出来的质数，那么奇数的答案就是小于等于3，如果奇数-2为质数，那么就取最小值2，其他情况为3.
（就当补充知识树了~~

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#define maxn 5005
#define inf 1000000002
#define for_(i,n) for(ll (i)=1;(i)<=(n);i++)
#define mod 80112002
int n,m;
int is_prome(int n){
    for (int i = 2; i <=sqrt(n) ; ++i) {
        if(n%i==0)return 0;
    }
    return 1;
}
int main(){
    IOS
    cin>>n;
    if(is_prome(n)){cout<<1;return 0;}
    if(n%2==0)cout<<2;
    else{
        if(is_prome(n-2))cout<<2;
        else cout<<3;
    }
    return 0;
}

573B Bear and Blocks

传送门
镜像传送门
dp水题（迫真
1800
Limak是只小熊，他堆了一行塔，每座塔都有相应的高度，每次Limak可以把所有没有被完全包围的砖块摧毁，询问要多少次才能将所有塔摧毁（tm熊的力量！（滑稽））
什么是完全包围呢，如图：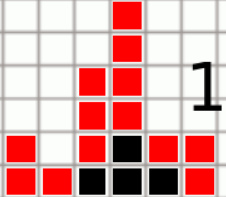
在这里插入图片描述
（黑色部分即为被完全包围的砖块。）
根据题意，我们可以很快得到几条规律：
1、高度为1的在第1轮就毁掉
2、第i座塔最多存活h[i]轮（每座塔最上面的砖块每轮必被摧毁）
3、从左向右扫，第i+1座塔最多比第i座塔多存活1轮，从右向左同理
现在转移方程就很好写了，开两个数组存分别存从左到右和从右到左（规律3）每座塔的存活轮数，那每个塔的存活轮数就是两个数组中对应位置的最小值，最后遍历每座塔取一个最大值就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#define maxn 100005
#define inf 1000000002
#define for_(i,n) for(ll (i)=1;(i)<=(n);i++)
#define mod 80112002
int n;
int h[maxn],l[maxn],r[maxn];
int main(){
    IOS
    cin>>n;
    for_(i,n)cin>>h[i];
    l[1]=r[n]=1;
    for_(i,n){
        if(i==1)continue;
        if(h[i]==1){
            l[i]=1;
        }else{
            l[i]=l[i-1]+1;
        }
        l[i]=min(l[i],h[i]);
    }
    for (int j = n-1; j >=1 ; --j) {
        if(h[j]==1)r[j]=1;
        else r[j]=r[j+1]+1;
        r[j]=min(r[j],h[j]);
    }
    int ans=-1;
    for_(i,n){
        //cout<<l[i]<<" "<<r[i]<<endl;
        ans=max(ans,min(l[i],r[i]));
    }
    cout<<ans;
    return 0;
}

374C Inna and Dima

点这里去这道题恰狗粮
点这里去恰镜像狗粮
dfs+dp（2000）
Inna和Dima买了一张n*m的桌子，每个格子里都写有D、I、M、A中某个字母，Inna特别爱Dima，所以Inna想从某个D开始按照D-I-M-A-D-I……的顺序经过尽量多完整的“DIMA”，如果一个都没有，那么输出“Poor Dima!”，如果可以一直走下去（存在环），输出“Poor Inna!”，否则输出最多能走的个数。
先处理给的方格图，对走向合法的组合连单向边，开个dp存到当前节点的最长路径长度，然后从每个D开始dfs就好，但是会T，加个剪枝就好了，如果下一个节点的dp可以更新，就dfs下一个节点。最后取所有A的最大值除以4即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios_base::sync_with_stdio(false);cin.tie(0);
#define maxn 1005
#define inf 1000000002
#define for_(i,n) for(ll (i)=1;(i)<=(n);i++)
#define mod 80112002
int dir[4]={1,-1,0,0},dir2[4]={0,0,1,-1};
int n,m;
struct node{
    int x,y;
};
node cc[maxn*maxn];
vector<int> g[maxn*maxn];
int d[maxn*maxn],num[maxn][maxn],vis[maxn*maxn],dp[maxn*maxn];
char s[maxn][maxn];
void link(int v){
    int x=cc[v].x,y=cc[v].y;
    for (int i = 0; i <4 ; ++i) {
        if(x+dir[i]<1||x+dir[i]>n||y+dir2[i]<1||y+dir2[i]>m)continue;
        int u=num[x+dir[i]][y+dir2[i]];
        if(s[x][y]=='D'&&s[x+dir[i]][y+dir2[i]]=='I'){g[v].push_back(u);d[u]++;}
        if(s[x][y]=='I'&&s[x+dir[i]][y+dir2[i]]=='M'){g[v].push_back(u);d[u]++;}
        if(s[x][y]=='M'&&s[x+dir[i]][y+dir2[i]]=='A'){g[v].push_back(u);d[u]++;}
        if(s[x][y]=='A'&&s[x+dir[i]][y+dir2[i]]=='D'){g[v].push_back(u);d[u]++;}
    }
}
void dfs(int x){
    vis[x]=1;
    for (auto i:g[x]){
        if(vis[i]&&s[cc[i].x][cc[i].y]=='D'){
            cout<<"Poor Inna!";
            exit(0);
        }
        if(dp[i]<dp[x]+1){
            dp[i]=max(dp[i],dp[x]+1);
            dfs(i);
        }
    }
    vis[x]=0;
}
int main(){
    IOS
    cin>>n>>m;
    for_(i,n)cin>>(s[i]+1);
    int cnt=1;
    for_(i,n){
        for_(j,m){
            num[i][j]=cnt;
            cc[cnt].y=j;
            cc[cnt++].x=i;
        }
    }
    for_(i,cnt){link(i);}
    queue<int> q;
    for_(i,cnt){
        if(s[cc[i].x][cc[i].y]=='D'){dp[i]=1;q.push(i);}
    }
    while(!q.empty()){
        int x=q.front();
        q.pop();
        dfs(x);
    }
    int ans=0;
    for_(i,cnt){
        if(s[cc[i].x][cc[i].y]=='A')ans=max(ans,dp[i]);
    }
    if(ans==0){cout<<"Poor Dima!";return 0;}
    cout<<ans/4;
    return 0;
}